Concept | Interpretation of regression model output#

This article discusses how to interpret regression model outputs in Dataiku.

Introduction#

In order to derive the most value from your predictive models, you need to know how to interpret the model quality assessment provided by Dataiku. It can get complicated because the error measure to take into account may depend on the business problem you want to solve.

Indeed, to interpret and draw conclusions from your analysis, you have to understand the basic concepts behind error assessment. Even more importantly, you have to think about the actions you will take based on your analysis.

In this article, we will go through metrics given when you use a regression model in Dataiku and how to interpret them in terms of a business application.

As an illustration, we will use the Boston housing dataset. It’s a textbook machine learning dataset, and it’s also a business application. The target we want to predict is house pricing as a function of features, such as the number of teacher per children or the distance to employment hubs. Finding the right price is essential to find a buyer in reasonable time and at the best price.

Note

To reproduce the following screenshots, upload the Boston housing dataset into a Dataiku project. Then create a quick prototype prediction model on the medv column. Train using the default settings.

Actual vs. predicted values scatter plot#

When you ask Dataiku to train a model, it begins by splitting your dataset into train and test sets. Click on a model in the first training session, and select the Training Information panel:

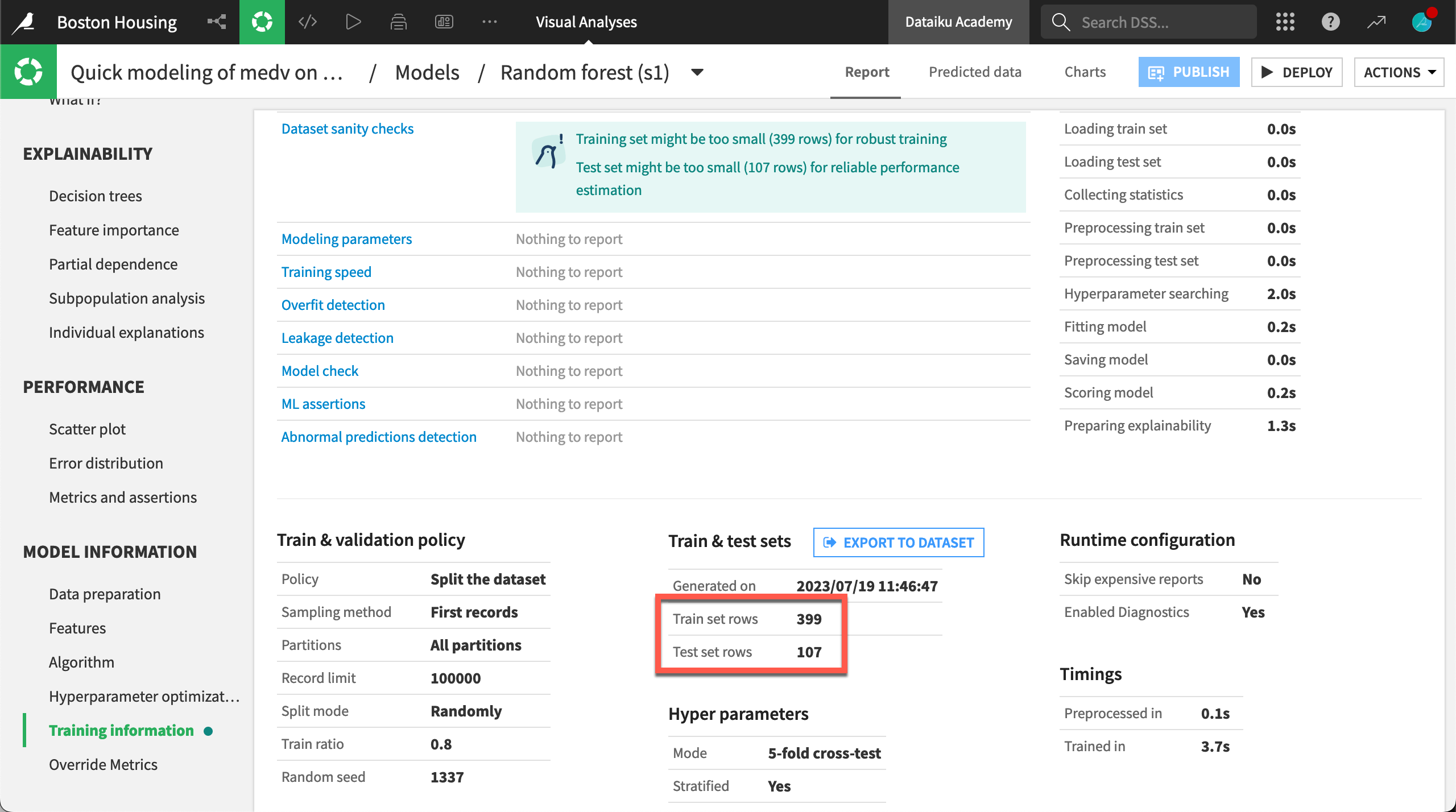
Dataiku screenshot of training information for a random forest model.

Dataiku optimizes model parameters on the train set and keeps the test set for assessing the model.

Next, head to the Scatter plot panel. For each point in the test set, the graph displays the actual value of the target on the x-axis and the value of the target predicted by the model on the y-axis.

If the model was perfect, all points would be on the diagonal line. This would mean that predicted values are exactly equal to actual values. The error on a data point is the vertical distance between the point and the diagonal. The point below the diagonal line are underestimated by the model and points above it are overestimated.

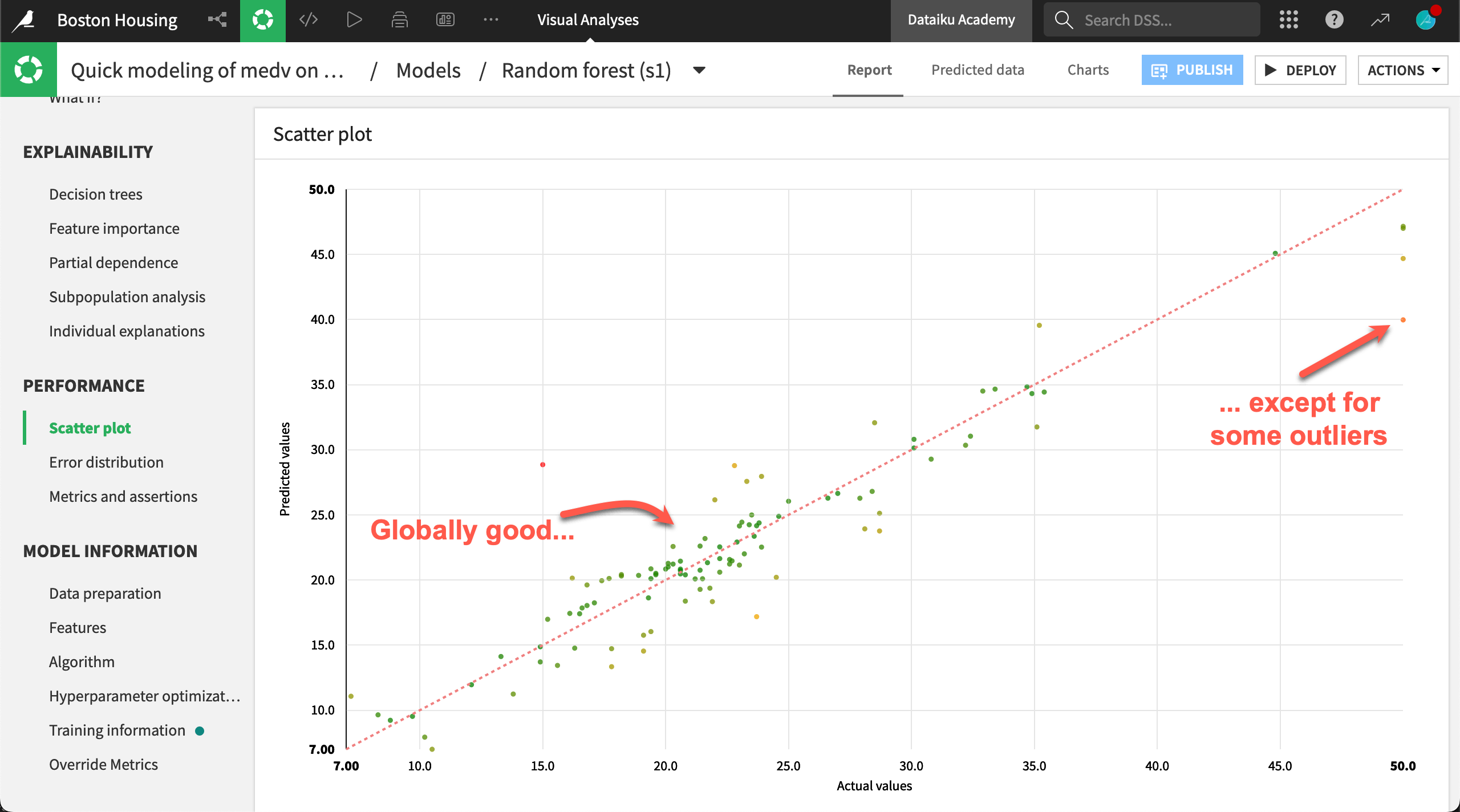
Dataiku screenshot of a Scatter plot of actual vs. predicted values.

You want to minimize the distance from the points to the diagonal (hence the error). However for some applications, overestimating can be way more problematic than underestimating.

An example would be predictive maintenance: Imagine you own a truck company and want to know when trucks are going to encounter failures. You want to repair them ahead of time, when they are at the garage and prevent failures from happening while on duty.

In this case, you should underestimate the time left before a failure happens to be sure to act on it properly. Overestimating means you won’t repair trucks in time, and that model would be useless. This perfectly illustrates the effect that errors can have when they are not symmetric.

Global scores#

If you return to the models results page, there is a field with an indicator that is a global measure of how good your model is. Dataiku provides you with all the standard statistical scores.

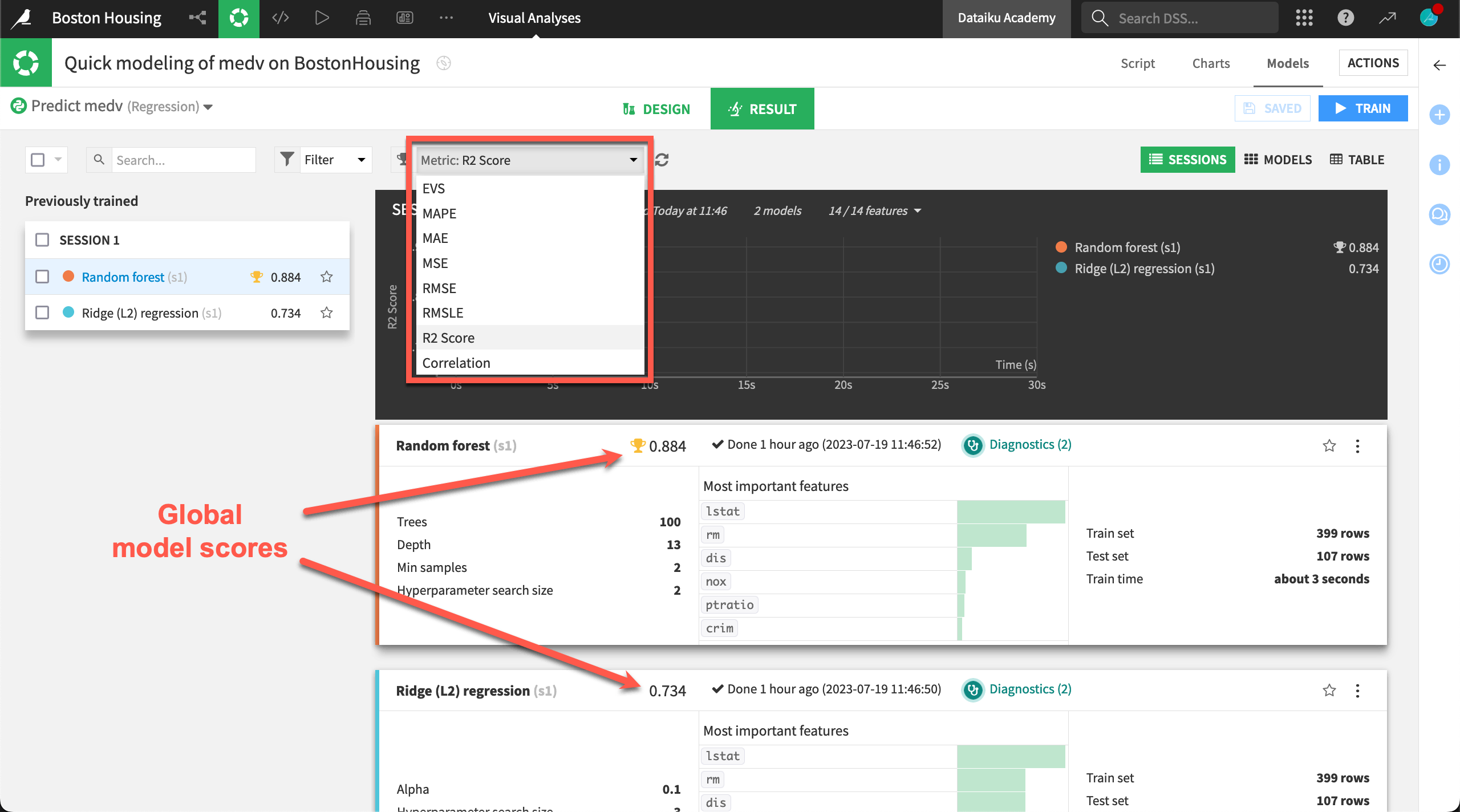
Dataiku screenshot of the models list page with arrows on the R2 score and on the selection of metrics.

Explained Variance Score, R2 score and Pearson correlation coefficient should be compared to 1 (the closer to 1 the better the model is).

The others (Mean Absolute Error, Mean Absolute Percentage Error, Mean Squared Error, Root Mean Squared Error, Root Mean Squared Logarithmic Error) are error measures, and should be as close as possible to zero.

If you click into a model report, and open the Metrics and assertions panel, you will see a list of scores. Each score is shortly defined. You can refer to Wikipedia entries for the detailed definitions of these scores.

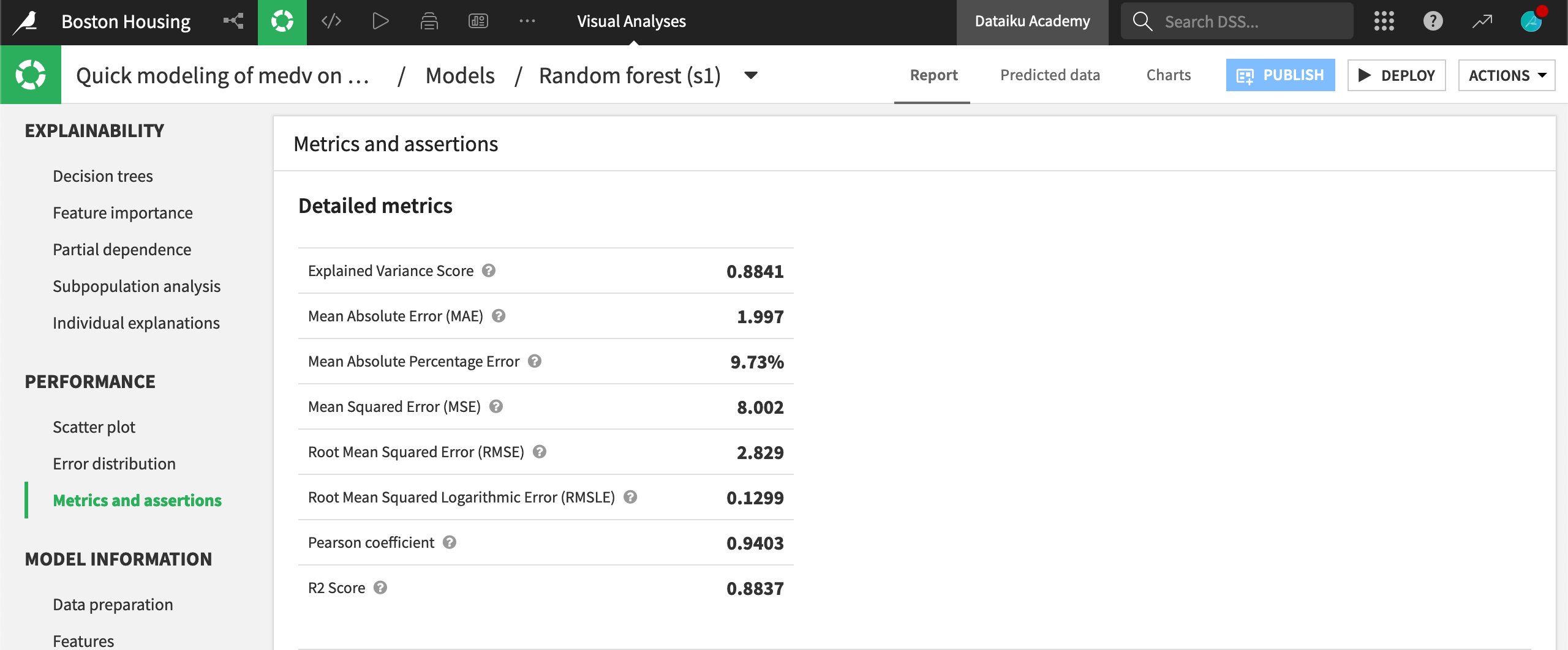
Dataiku screenshot of detailed metrics for a random forest model.

Here we will go through the scores, give an interpretation, and develop, if possible, an implication in terms of business.

  • Pearson coefficient: Correlation assesses to what extent two variables vary simultaneously. If the variables increase at the same time, they are said to correlate. Inversely, if one variable increases, while the other decreases, they anti-correlate. In our case, the correlation coefficient is computed between the predicted and the actual values. Hence, the closer the correlation is to 1, the better the model.

  • R2 (coefficient of determination) is the square of the Pearson coefficient.

  • Explained Variance Score gives you the fraction of what your model is able to explain of your target. If you may, it’s the fraction of what the model knows compared to all there is to know about your target.

  • Mean Squared Error and Root Mean Squared Error: The variance of the error and the standard deviation of the error. If the model error is normally distributed (check the error distribution to know that), multiplying the standard deviation by three, you will obtain a very safe interval of how big your error can be. The problem with this error is that it is very sensitive to outliers. This means that if you have a very good model with a large error only for one data point (that might be a measurement error), this score will be high.

  • Mean Absolute Error (MAE): An alternative to the outlier-sensitive MSE is the MAE. Because it takes the absolute value of the error, the effect of one outlier won’t be as drastic as for RMSE.

  • Mean Average Percentage Error is an interesting metric. Instead of measuring the simple discrepancy between predicted values and actual values, it gives the error in percentage of the value itself. This means that an error of $10,000 on a flat costing $200,000 is considered equivalent to an error of $100,000 on a mansion costing $2,000,000. This seems particularly appropriate for pricing targets.

  • Construct your custom metric: The metrics above makes sense in most cases, but depending on what you want to do, you may need to create a custom metric. Going back to our predictive maintenance example with trucks, you could implement a score that is the global price of repairs for the next year. Every time your model predicts the failure before it happens, your cost is a simple repair. However if the predicted failure happens after the actual failure, you will pay for the repair and the price of retrieving the truck! Of course, you don’t want to put your truck in repairs every two days. So your score should take the frequency of interventions on a single truck into account.